A je to tady. Zase! Nebojte, zatím mě ještě nevezou do Bohnic. Pojmem zbláznil jsem se označuji okamžiky v mé tvorbě, kdy se v podstatě ze dne na den rozhodnu pracovat na něčem novém.

Už se to stalo několikrát ... vlastně když nad tím tak přemýšlím, tak se to tak stalo u cca 90% mých projektů. Někdy se jednalo o něco malého, ale někdy to byl nový jazyk a s ním nový velký projekt - např. Elfánie. A velké je to i tentokrát. Dovolím si říct, že je to zatím největší.

Point in polygon (bod v mnohoúhelníku)

Vraťme se zpět ještě do doby před mojí maturitou. Všechno to začalo v hodině angličtiny. V druhém pololetí jsme se učili pouze měsíc a pak ti, kteří z ní nematurovali, měli volno. Já ho začal využívat programováním. Notebook se mi do školy tahat nechtělo a jelikož mám bluetooth klávesnici, tak jsem ji připojil k mobilu a programoval na mobilu.

V úterý jsme mívali před angličtinou tělocvik a tak tomu bylo i toho dne. Já se jako obvykle lajdal v posilovně, kam učitel chodíval na kontrolu málokdy (a stejně dobře věděl, že tam nic nedělám). Čas jsem tam trávil přemýšlením, většinou o tom, co jsem se chystal programovat, až přijdu domů.

Jednou mě napadl takový problém (opravdu si už nepamatuji, jakými myšlenkovými pochody jsem k němu dospěl). Když mám definovaný libovolný polygon (mnohoúhelník) a libovolný bod, tak jak by vypadal algoritmus pro zjištění, jestli se bod nachází vně, nebo uvnitř polygonu.

Do tohoto problému jsem se ponořil na tolik, že jsem o něm přemýšlel ještě dobu o angličtině místo programování. Několik nápadů na řešení jsem dostal, ale žádný mi nepřišel moc elegantní. Na konec jsem to vzdal a zkusil zabrouzdat po internetu. Řešení jsem našel na Wikipedii:

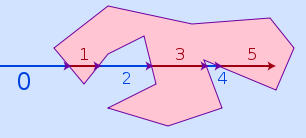
Řešení spočívá v tom, že bodem povedeme přímku (kterým směrem je jedno, nejjednodušeji by se to počítalo na ose x nebo y). Potom vypočítáme body průniku se všemi stranami polygonu (pokud existují) a pak těmito průniky rozdělíme naši přímku. Jednotlivé části očíslujeme (od nuly, jak je v programování zvykem). A nakonec se stačí podívat, v kolikáté části se nachází náš bod. Pokud se nachází v sudé, je mimo polygon, pokud v liché, je uvnitř.

Samozřejmě ještě mohou nastat problémy s tím, když bude daná přímka procházet přeš vrchol, nebo hrana polygonu bude ležet na této přímce, ale to není důležité řešit, abyste tento algoritmus pochopili.

Geometrie

Doma jsem přemýšlel nad dalšími problémy týkající se geometrie, např. nad tím, jak u libovolného polygonu vypočítat těžiště. Nakonec jsem přišel na to, že by bylo nejlepší si ten polygon rozdělit na trojúhelníky, u nich se spočítá těžiště jednoduše - průměr vrcholů. A pak, když chci těžiště celého polygonu, stačí spočítat vážený průměr (podle obsahů) z těžišť trojúhelníků.

No nevím, co si teď o mě myslíte, když přemýšlím nad takovýma kravinama, ale má to smysl, čtěte dál, důvod se dozvíte o pár odstavců později.

Samozřejmě jsem dostal strašnou chuť si to naprogramovat. Tuto chuť dostávám velmi často, ale většinou mě přejde - jsem od přírody líný člověk a kdybych programoval všechno, co mě napadne, tak nedělám nic jiného. Ale občas nějakou blbost naprogramuju a někdy se dostanu tak daleko, že ji dokonce zveřejním, viz Vesmír.

Jistě tušíte, že u tohoto na programování došlo. Jenže jsem nevěděl, který z problémů si vybrat. Řešení mě napadlo vzápětí - udělat si univerzální API (programové rozhraní = třídy, pokud víte, co je OOP...), na kterém následně budu moct řešit všechny problémy. A tak vznikl nový projekt s názvem Geometrie. Proč jsem zvolil univerzální řešení mělo ještě jeden důvod, brzy se dozvíte, jaký.

Jako jazyk jsem si zvolil JavaScript, protože ten je pro mě nejvíce user-friendly - Chrome má skvělou JS konzoli, ve které si to mohu bez omezení testovat. Ale brzy jsem začal poznávat, že to není ideální volba - v JavaScriptu nepoužívám prototypy, takže se musím obejít bez dědičnosti, což zrovna u Geometrie není dobré. A tak jsem dostal nápad si to zkusit napsat v C++, které jsem si nedávno zkoušel - udělal jsem nový generátor Sudoku, ale bohužel jsem ho už nedotáhl do konce a učení C++ jsem odložil na později (podle původního plánu na pomaturitní období).

C++, tentokrát doopravdy

Dřív jsem si s C++ pouze hrál a do žádných složitostí jsem nešel, tudíž mi stačily zkušenosti z C#, ale teď, když jsem si chtěl udělat třídy s dědičnostmi, jsem začal narážet na první problémy. Asi největší problém byl, že jsem absolutně neznal céčkovské prototypy a nevěděl jsem, jak kompilátor zpracovává zdrojové soubory. Byl jsem zvyklý z C#, že si to kompilátor sám nějak vyřeší, ale u C++ to tak moc neplatí a programátor musí v některých věcech vycházet kompilátoru vstříc - například psát již zmíněné prototypy, aby kompilátor věděl o existenci funkce - kompilátor se sám nepodívá dál do kódu, aby si o funkci něco zjistil - ale platí to jen u funkcí (které C# ani nemá) a tříd, u metod v rámci jedné třídy ne.

Problém s chybami (které jsem tehdy nechápal) jsem sice vyřešil, ale cítil jsem, že moje řešení nejspíš není moc dobré, takže jsem se rozhodl, že se C++ naučím pořádně, tedy že si koupím knížku. A když jsem řekl pořádně, rozhodl jsem se koupit tu největší, a tak jsem si koupil knihu (to už není knížka :D) Mistrovství v C++ a rázem jsem měl přes 1000 stran ke čtení, do kterého jsem se ihned pustil (vlastně ne ihned, ale ještě dříve, než mi přišla - na Uložtu je téměř vše...).

A když uvážíte, že v této době mi zbývalo posledních pár dní do maturity, tak asi už pochopíte nadpis tohoto článku (i když toto ještě není přesně to, co jsem tím nadpisem myslel).

O C++ bych rád napsal ještě mnohem víc, ale pro dnešní článek by toto mohlo stačit - délka článku se opět začíná blížit kilometru. Nebojte, určitě vás o to neochudím - nechám si to na příští článek (respektive články).

K čemu to?

O pár odstavců výš jsem vám slíbil, že vám prozradím důvod, proč jsem nad Geometrií přemýšlel a následně ji začal programovat. Ano, týká se to programování, ale nové verze Elfánie ne. Už dlouho totiž přemýšlím nad tím, jak udělám druhou epizodu Lojzika. Při programování první epizody jsem udělal mnoho chyb (od zvolení programovacího jazyka až po návrh toho, jak to vevnitř funguje). Jedna z věcí, která se mi na první epizodě opravdu nelíbí je pohyb Lojzika, jelikož o něm (a všech ostatních postavách) jsem přemýšlel jako o obdélnících a uvažte sami - lidé nejsou obdelníkům moc podobní. Na první problémy jsem začal narážet již ze začátku vývoje, ale tehdy jsem nebyl schopen to moc řešit. Díky tomu vznikala spousta grafických chyb, které jsem se snažil co nejvíce minimalizovat, ale i přesto některé opravit prostě nešly.

S knihovnou Geometrie budu moct daleko lépe řešit kolize objektů (mnohoúhelník lépe popisuje realitu než obdelník) a dokonce vypočítávat i jemné pohyby místo sady obrázků pro pohyb postavy, které se vykreslují nad pomyslným obdelníkem.

Později jsem začal o potenciálu Geometrie přemýšlet i mimo Lojzika a samotného mě začalo překvapovat, co všechno bych s touto knihovnou mohl dokázat naprogramovat. Například... znáte Angry Birds? Ne, nezačal jsem si programovat vlastní verzi naštvaných ptáků, pouze je uvádím jako příklad využití.

No a to by dnes mohlo stačit, těšte se na další část!

PS: Nejspíš jsem zapomněl na spoustu věcí, které jsem chtěl zmínit - musím si udělat TODO, abych na ně už příště nezapomněl.